Conceptos orthogonal y perspectiva con ejemplos

Proyección en opengl (ortogonal y perspectiva)

Una proyección ortogonal define un volumen de la vista de tipo paralelepipédico tal y como se muestra en la siguiente figura. La principal característica de esta proyección es que el tamaño de los objetos es independiente de la distancia a la que estén del observador, por ejemplo, dos cilindros del mismo tamaño, uno a cinco unidades y el otro a diez unidades de distancia del observador se proyectarán con el mismo tamaño.

Aunque OpenGL dispone de pilas para

Las matrices GL_MODELVIEW y GL_PROJECTION, sólo se suele utilizar la pila de

GL_MODELVIEW.

 

Para definir una proyección ortogonal en OpenGL hay que dar los siguiente pasos:

glMatrix(GL_PROJECTION); /* Voy a manejar la matriz de proyección */
glLoadIdentity(); /* Cargo inicialmente la identidad */
/* Y ahora defino la proyección ortogonal */
void glOrtho(izquierda, derecha, abajo, arriba, cerca, lejos);

Si lo que deseamos es trabajar con una proyección ortogonal 2D:

void gluOrtho2D(izquierda, derecha, abajo, arriba);

que no es más que una proyección ortogonal donde el plan delantero está en -1 y el trasero en 1.

Por ejemplo, la ilustración 1.2 es un render de un coche con proyección ortográfica, visto desde delante.

                                                             Imagen 1.2

 

El código utilizado para esta proyección ha sido

glOrtho(-0.5f, 0.5f, -0.5f, 0.5f, 0.01f, 20.0f

Proyección perspectiva

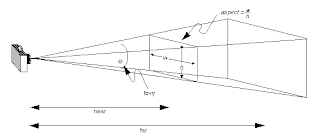
La proyección ortogonal no da sensación de profundidad porque el tamaño de los objetos no depende de su distancia al observador. Para conseguir este efecto necesitamos definir una proyección perspectiva. Esta proyección define un volumen de la vista que es una prisma truncado de base rectangular, como el de la siguiente figura:

 

 

la función OpenGL que establece este tipo de perspectiva es:

void glFrustum(izquierda, derecha, abajo, arriba, cerca, lejos);

este modo de definir la proyección perspectiva no es demasiado intuitivo, es más sencillo establecerla con un esquema como el que se muestra en la siguiente figura:

y la función OpenGL que la establece es:

La función OpenGL que establece el tamaño del vierport es:

void glViewport(GLint x, GLint y, GLsizei ancho, GLsizei alto);

La ilustración 1.3 muestra la escena del coche de la sección anterior, esta vez con una proyección en perspectiva:

                                                          Ilustracion 1.3

 

El código utilizado para definir la proyección ha sido:

gluPerspective(45.0f,(GLfloat)(width/height),0.01f,100.0f);

Se usan 45º de ángulo, la relación entre el ancho y alto de la pantalla (width y height son el ancho y alto actual de la ventana) y las distancias a los planos de corte znear y zfar son 0.01 y 100 respectivamente.

Un poco mas complejo es este

// Le digo a OpenGL que voy a cambiar la matriz de proyeccion

glMatrixMode(GL_PROJECTION);

// Le digo a OpenGL que use proyeccion perspectiva. Uso el ancho

// y alto de mi viewport para calcular el segundo parametro

gluPerspective(60.0f, (float)rect.right/(float)rect.bottom, 0.5f, 50.0f);

// Muevo para atras el objeto. El punto de vista esta

// en la posicion 0,0,0 porque no lo he cambiado, asi que

// alejo el objeto para poder verlo.

glTranslatef(0,0,-4.0f);

// Giro el objeto 30 grados en el eje x, luego otros

// 30 en el eje y. Es para que quede bonito.

glRotatef(30,1,0,0);

glRotatef(30,0,1,0);

 

// y pinto el objeto con coordenadas genericas alrededor

// del eje de coordenadas. Estas coordenadas que pongo

// ahora son modificadas por las modificaciones que

// hemos hecho en la matriz modelview (glTranslate, glRotate).

 

// Le digo a OpenGL que voy a pintar y con cuadrados:

glBegin(GL_QUADS);

// Cara de arriba

glColor3f(1,0,0); // rojo

glVertex3f( 1.0f, 1.0f,-1.0f);   

glVertex3f(-1.0f, 1.0f,-1.0f);   

glVertex3f(-1.0f, 1.0f, 1.0f);   

glVertex3f( 1.0f, 1.0f, 1.0f);   

// Cara de abajo

glColor3f(1,0,0); // rojo

glVertex3f( 1.0f,-1.0f, 1.0f);   

glVertex3f(-1.0f,-1.0f, 1.0f);   

glVertex3f(-1.0f,-1.0f,-1.0f);   

glVertex3f( 1.0f,-1.0f,-1.0f);   

// Cara frontal

glColor3f(0,0,1); // azul

glVertex3f( 1.0f, 1.0f, 1.0f);   

glVertex3f(-1.0f, 1.0f, 1.0f);   

glVertex3f(-1.0f,-1.0f, 1.0f);   

glVertex3f( 1.0f,-1.0f, 1.0f);

// Cara trasera

glColor3f(0,0,1); // azul

glVertex3f( 1.0f,-1.0f,-1.0f);   

glVertex3f(-1.0f,-1.0f,-1.0f);   

glVertex3f(-1.0f, 1.0f,-1.0f);   

glVertex3f( 1.0f, 1.0f,-1.0f);

// Cara izquierda

glColor3f(0,1,0); // verde

glVertex3f(-1.0f, 1.0f, 1.0f);   

glVertex3f(-1.0f, 1.0f,-1.0f);   

glVertex3f(-1.0f,-1.0f,-1.0f);   

glVertex3f(-1.0f,-1.0f, 1.0f);

// Cara derecha

glColor3f(0,1,0); // verde

glVertex3f( 1.0f, 1.0f,-1.0f);   

glVertex3f( 1.0f, 1.0f, 1.0f);   

glVertex3f( 1.0f,-1.0f, 1.0f);   

glVertex3f( 1.0f,-1.0f,-1.0f);

glEnd();

 

 

Transformaciones Geométricas (EJEMPLOS DE TRASLACION, ROTACION Y ESCALADO)

Traslacion

void dibujar_triangulo(){

glBegin(GL_TRIANGLES)

glVertex3f(0,0,0);

glVertex3f(1,0,0);

glVertex3f(0,1,0);

glEnd();

}

// dibuja el triangulo en la posición original

Dibujar_triángulo();

// dibuja el triangulo desplazado

glTranslate(10,0,0);

Dibujar_triángulo();
<!--[if !supportLineBreakNewLine]-->
<!--[endif]-->

Rotacion y escalacionglMatrixMode(GL_MODELVIEW);

glLoadIdentity();

glRotate(45,0,0,1);

glTranslate(10,0,0)

glScale(2,2,2)

Dibujar_triangulo();

glLoadIdentity();

glRotate(45,0,0,1);

glTranslate(0,10,0)

glScale(2,2,2)
Dibujar_cuadrado();
<!--[if !supportLineBreakNewLine]-->
<!--[endif]-->

Manejo de matrices en opengl para Para proyeccion y para modelado

Proyeccion

La matriz de proyección especifica el tamaño y la forma del volumen de visualización. El volumen de visualización es aquel cuyo contenido es el que se representa en pantalla. Está delimitado por una serie de planos de trabajo. De estos planos, los más importantes son los planos de corte, que son los que nos acotan el volumen de visualización por delante y por detrás. En el plano más cercano a la cámara (znear) es donde se proyecta la escena para luego pasarla a la pantalla.

Modelado

La matriz del modelador es una matriz 4x4 que representa el sistema de coordenadas transformado que se está usando para colocar y orientar los objetos. Si se multiplica la matriz del vértice (de tamaño 1x4) por ésta se obtiene otra matriz 1x4 con los vértices transformados sobre ese sistema de coordenadas.

RESUMEN

PIla de Matrices

En la función display() se encuentran las llamadas a dos funciones de matrices que todavía no han sido comentadas. Se trata de glPushMatrix() y glPopMatrix(). Para comprender su funcionamiento, primero se va a experimentar que es lo que ocurre cuando no están dichas llamadas. Para ello se comentan en la función display() ambas llamadas:

void display(void) {

// glPushMatrix();

glTranslatef(0.0, 0.0, .5);

...

// glPopMatrix();

glutSwapBuffers();

}

 

La razón de este movimiento es que en la función display está incluida una llamada a glTranslatef() que se utiliza para posicionar uno de los objetos. Como se ha explicado anteriormente, las funciones de traslación multiplican la matriz actual por una matriz de traslación creada con los argumentos que se le pasan, por tanto, sucesivas llamadas a la función display() provocan sucesivas multiplicaciones de la matriz actual con el efecto que se observa de incrementar la traslación. Para solucionar este problema OpenGL dispone de unos stacks o pilas de matrices, que permiten almacenar y recuperar una matriz anterior. aunque opengl dispone de pilas para las matrices gl_modelview y gl_projection, sólo se suele utilizar la pila de gl_modelview. Una pila es un almacén con funcionamiento LIFO, el último en entrar es el primero en salir, por lo que suele comparar a una pila de platos en la que sólo se puede dejar uno encima de la pila o coger el superior que es el último depositado. La pila de matrices tiene el mismo funcionamiento sustituyendo los platos por matrices. La matriz superior de la pila es sobre la que se aplican las distintas transformaciones, multiplicándola por la matriz que generan las disntintas funciones.

La función glpushmatrix() realiza una copia de la matriz superior y la pone encima de la pila, de tal forma que las dos matrices superiores son iguales.. Las siguientes transformaciones que se realizan se aplican sólo a la matriz superior de la pila, quedando la anterior con los valores que tenía en el momento de llamar a la función glpushmatrix(). La función glpopmatrix() elimina la matriz superior, quedando en la parte superior de la pila la matriz que estaba en el momento de llamar a la función glpushmatrix().

 

Necesitaremos realizar tres operaciones: calcular la coordenadas donde se encuentra la tortuga, almacenar dicha coordenada y dibujar el rastro. Para almacenar los puntos se utiliza una variable para indicar el número de puntos y tres vectores para las coordenadas x, y, z.

int np = 0;

float px [10000];

float py [10000];

float pz [10000];

Para calcular las coordenadas de la tortuga es necesario conocer la matriz de transformación de modelado. Debido a que en OpenGL, la matriz de modelado se almacena junto con la de visualización en la matriz GL_MODELVIEW, es necesario guardar de modo independiente esta matriz de modelado. Para ello definimos la variable mModel, como una variable global, ya que va a ser accedida en distinos puntos de la aplicación.

glmatrixmode(gl_modelview);

glpushmatrix();

glLoadIdentity();

glgetdoublev (gl_modelview_matrix, mmodel);

glPopMatrix();

En este código se realizan las siguientes operaciones:

<!--[if !supportLists]-->· <!--[endif]-->œ se indica primeramente sobre que matriz se van a realizar las opereraciones con glMatrixMode();

<!--[if !supportLists]-->· <!--[endif]-->œ se crea una nueva matriz con glPushMatrix();

<!--[if !supportLists]-->· <!--[endif]-->œ se carga la matriz identidad con glLoadIdentity();

<!--[if !supportLists]-->· <!--[endif]-->œ se almacena la matriz superior de la pila en el vector mModel con la función glGetDoublev();

<!--[if !supportLists]-->· <!--[endif]-->œ y finalmente se elimina la matriz superior de la pila con glPopMatrix() para dejar la

que estaba antes de este proceso.

En realidad todo este proceso lo que ha hecho ha sido inicializar la matriz que represena

mModel con la matriz identidad. La función glMultMatrixd() multiplica la matriz superior de la pila por la matriz que tiene como argumento. Al multiplicar en este caso por la matriz identidad, la matriz que queda en la posición superior de la pila es mModel. La llamada a addPointToTrace() se introduce despues de las llamadas a gltranslatef() en las instrucciones correspondientes al forward y back. addPointToTrace();

La llamada a displayTrace() se realiza en la función display(). El dibujo del objeto que representa la tortuga se debe realizar despues de multiplicar la matriz actual (la matriz de visualización) por la matriz de modelado que se almacena en mModel. Dibujar un rastro que consista en unas superficie en lugar de una línea. Para ello se puede utilizar glBegin(GL_QUAD_STRIP) que dibuja una sucesión de rectángulos para cada pareja de puntos que recibe.

 

Mostrar el texto

Las instrucciones introducidas se muestran en la ventana MSDOS. Se pueden mostrar en la ventana gráfica. Para ello es necesario cambiar las matrices de transformación. La siguiente función realiza la representación del texto:

void text(GLuint x, GLuint y, GLfloat scale, char* format, ...) {

va_list args;

char buffer[255], *p;

GLfloat font_scale = 119.05f + 33.33f;

va_start(args, format);

vsprintf(buffer, format, args);

va_end(args);

glMatrixMode(GL_PROJECTION);

glPushMatrix();

glLoadIdentity();

gluOrtho2D(0, glutGet(GLUT_WINDOW_WIDTH), 0,

glutGet(GLUT_WINDOW_HEIGHT));

glMatrixMode(GL_MODELVIEW);

glPushMatrix();

glLoadIdentity();

glPushAttrib(GL_ENABLE_BIT);

glDisable(GL_LIGHTING);

glDisable(GL_TEXTURE_2D);

glDisable(GL_DEPTH_TEST);

glTranslatef(x, y, 0.0);

glScalef(scale/font_scale, scale/font_scale, scale/font_scale);

for(p = buffer; *p; p++)

glutStrokeCharacter(GLUT_STROKE_ROMAN, *p);

glPopAttrib();

glPopMatrix();

glMatrixMode(GL_PROJECTION);

glPopMatrix();

glMatrixMode(GL_MODELVIEW);

}

Para mostrar el texto se llama desde la función display() con la sentencia:

if (command) {

glColor3f(1.0,1.,0.0) ;

text(5, 5, 20, "->%s", strCommand);

PUNTOS A REALIZAR

Utilizando los comandos de logo representar una esfera compuesta por un

conjunto de circunferencias en el espacio.

Utilizando los comandos de logo

realizar la representación de una

helicoidal.

La transformación de puerto de vista:

Esta transformación define el tamaño y la posición de la imagen final (como la impresión de una fotografía), se usa el comando glViewPort() y es necesario modificar el puerto de vista cada que la ventana se modifica.

Una vez que todas estas transformaciones son aplicadas a cada uno de los vértices, la imagen puede ser desplegada dentro de la ventana.

La sintaxis de los comandos de transformación es la siguiente:

glTranslate {fd} (TYPE x, TYPE y TYPE z);

glRotate {fd} (TYPE ángulo,TYPE x, TYPE y, TYPE z);

glScale {fd} (TYPE x, TYPE y, TYPE z);

En donde TYPE es float o int, dependiendo del comando que se escogió.

10.- Normales, Color e Iluminación:

glColor3 {b,s,i,f,d} (TYPE rojo, TYPE verde, TYPE azul)

 

 

Un ejemplo de esto es el siguiente:

glBegin(GL_POLYGON);

        glNormal3fv(n0);        /* n0 es un arreglo que contiene los datos */

        glVertex3fv(v0);

        glNormal3fv(n1);

        glVertex3fv(v1);

        glNormal3fv(n2);

        glVertex3fv(v2);

glEnd();

 

__________________________________________________________________________________
Cubo y Piramide Modificada

#include <GL/glut.h>

GLfloat anguloCuboX = 0.0f;
GLfloat anguloCuboY = 0.0f;
GLfloat anguloEsfera = 0.0f;

GLint ancho=600;
GLint alto=600;

int hazPerspectiva = 0;

void reshape(int width, int height)
{
glViewport(0, 0, width, height);
glMatrixMode(GL_PROJECTION);
glLoadIdentity();

if(hazPerspectiva)
gluPerspective(60.0f, (GLfloat)width/(GLfloat)height, 1.0f, 20.0f);
else

glOrtho(-4,4, -4, 4, 1, 10);

glMatrixMode(GL_MODELVIEW);

ancho = width;
alto = height;
}

void drawCube(void)
{
glColor3f(1.0f, 0.0f, 0.0f);
glBegin(GL_QUADS); //cara frontal
glVertex3f(-1.0f, -1.0f, 1.0f);
glVertex3f( 1.0f, -1.0f, 1.0f);
glVertex3f( 1.0f, 1.0f, 1.0f);
glVertex3f(-1.0f, 1.0f, 1.0f);

glEnd();

glColor3f(0.0f, 1.0f, 0.0f);

glBegin(GL_QUADS); //cara trasera
glVertex3f( 1.0f, -1.0f, -1.0f);
glVertex3f(-1.0f, -1.0f, -1.0f);
glVertex3f(-1.0f, 1.0f, -1.0f);
glVertex3f( 1.0f, 1.0f, -1.0f);

glEnd();

glColor3f(0.0f, 0.0f, 1.0f);
glBegin(GL_QUADS); //cara lateral izq
glVertex3f(-1.0f,-1.0f, -1.0f);
glVertex3f(-1.0f,-1.0f, 1.0f);
glVertex3f(-1.0f, 1.0f, 1.0f);
glVertex3f(-1.0f, 1.0f, -1.0f);
glEnd();

glColor3f(1.0f, 1.0f, 0.0f);
glBegin(GL_QUADS); //cara lateral dcha
glVertex3f(1.0f, -1.0f, 1.0f);
glVertex3f(1.0f, -1.0f, -1.0f);
glVertex3f(1.0f, 1.0f, -1.0f);
glVertex3f(1.0f, 1.0f, 1.0f);
glEnd();
glColor3f(0.0f, 1.0f, 1.0f);
glBegin(GL_QUADS); //cara arriba
glVertex3f(-1.0f, 1.0f, 1.0f);
glVertex3f( 1.0f, 1.0f, 1.0f);
glVertex3f( 1.0f, 1.0f, -1.0f);
glVertex3f(-1.0f, 1.0f, -1.0f);
glEnd();

glColor3f(1.0f, 0.0f, 1.0f);
glBegin(GL_QUADS); //cara abajo
glVertex3f( 1.0f,-1.0f, -1.0f);
glVertex3f( 1.0f,-1.0f, 1.0f);
glVertex3f(-1.0f,-1.0f, 1.0f);
glVertex3f(-1.0f,-1.0f, -1.0f);
glEnd();
}

void display()
{
glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT);

glLoadIdentity();

glTranslatef(0.0f, 0.0f, -5.0f);
glTranslatef(-3,0,0);
glRotatef(anguloCuboX, 1.0f, 0.0f, 0.0f);
glRotatef(anguloCuboY, 0.0f, 1.0f, 0.0f);
glScalef(0.5f, 0.5f, 0.5f);
drawCube();

glLoadIdentity();

glTranslatef(0.0f, 0.0f, -5.0f);
glRotatef(anguloEsfera, 0.0f, 1.0f, 0.0f);
glTranslatef(3.0f, 0.0f, 0.0f);

glColor3f(1.0f, 1.0f, 1.0f);
glutWireSphere(0.5f, 8, 8);

glFlush();
glutSwapBuffers();

anguloCuboX+=0.1f;
anguloCuboY+=0.1f;
anguloEsfera+=0.2f;
}

void init()
{
glClearColor(0,0,0,0);
glEnable(GL_DEPTH_TEST);
ancho = 600;
alto = 600;
}


void idle()
{
display();
}

void keyboard(unsigned char key, int x, int y)
{
switch(key)
{
case 'p':
case 'P':
hazPerspectiva=1;
reshape(ancho,alto);
break;

case 'o':
case 'O':
hazPerspectiva=0;
reshape(ancho,alto);
break;

case 27: // escape
// exit(0);
break;
}
}

int main(int argc, char **argv)
{
glutInit(&argc, argv);
glutInitDisplayMode(GLUT_DOUBLE | GLUT_RGB);
glutInitWindowPosition(100, 100);
glutInitWindowSize(ancho, alto);
glutCreateWindow("Cubo 1");
init();
glutDisplayFunc(display);
glutReshapeFunc(reshape);
glutIdleFunc(display);
glutKeyboardFunc(keyboard);
glutMainLoop();
return 0;
}

Corrida

Algoritmo DDA

 

Y=1.5*X-1

Presentacion Transformaciones Geometricas

Rotaciones 2D

La rotación de un objeto en 2D se lleva a cabo alrededor de un punto, que es el eje puntual (cero-dimensional) de rotación. Las rotaciones principales 2D son aquellas que se llevan a cabo alrededor del origen, las rotaciones sobre cualquier otro punto arbitrario se llaman  rotaciones  generales  2D.  En  esta  Sección  3.5  ,  se  analizan  sólo  las  rotaciones principales  para  todas  las  dimensiones,  en  la  Sección  3.6 se  discuten  las  rotaciones generales.

Para generar una rotación, se especifica el ángulo de rotación 0, y el punto de rotación (pivote) sobre el cual el objeto será rotado. Los ángulos de rotación positivos definen una rotación en sentido contrario a las manecillas del reloj sobre el punto pivote (del eje X1 al eje X2), entonces los ángulos de rotación negativos producen una rotación en el sentido de las manecillas (del eje X2 al eje X1). [Hearn 95] describe la rotación 2D como el giro sobre el eje de rotación que es perpendicular al plano X1X2 (mejor conocido como plano XY) y que pasa a través del punto pivote.

 

Aplicando algunas propiedades trigonométricas:

                       x1 ' = r cos(Ø + 0 ) = r cosØ cos0 − r sin Ø sin0

                      x2 ' = r sin(Ø + 0 ) = r cosØ sin0 + r sin Ø cos 0  

         

 Substituyendo los valores de  x1 = r cos(Ø )  y  x2 = r sin(Ø ) se obtienen las ecuaciones para rotar un punto  p = (x1, x2 ) alrededor del origen dado un ángulo Ø:

 

                                 x1 ' = x1 cos 0 − x2 sin 0

                                 x2 '= x1 sin 0+ x2 cos0

muestra el efecto de rotación de una figura con 0 = 45°

Translación 2D

La translación 2D implica el desplazamiento de un polígono, donde cada punto p = (x1 , x2 ) es trasladado d1 unidades en el eje X1 y d2 unidades en el eje X2, de esta forma, las coordenadas del nuevo punto p' = (x1 ', x2 ' ) , se obtienen como:

x1 ' = x1 + d1

x2 ' = x2 + d 2

Sea d = (d1 , d 2 ) el vector de distancias, y T(d) la matriz de translación, en coordenadas homogéneas la translación de un punto p en 2D se puede expresar como el producto matricial p' = p ⋅ T (d ) , es decir:

La Figura 3.3 muestra el efecto de translación de una figura con d1 = 1 y d2 = 2.

 

 

 

 

 

 

 

Escalamiento en 2D

El escalamiento permite cambiar el tamaño de un objeto expandiéndolo o contrayéndolo en sus dimensiones.

Sea s = (s1, s2) el vector de factores de escalamiento, y S(s) la matriz de escalamiento, en coordenadas homogéneas el escalamiento de un punto p en 2D se puede expresar como el producto matricial p' = p ⋅ S (s), es decir:

muestra el efecto de escalamiento de una figura con s1 = 1.5 y s2 = 2

 

 

 

 

 

 

2.2. Coordenadas homogéneas y representación matricial

En las aplicaciones de diseño y de creación de imágenes, realizamos traslaciones, rotaciones y escalaciones para ajustar los componentes de la imagen en sus posiciones apropiadas. En este tema consideramos cómo se pueden volver a formular las representaciones de la matriz de modo que se pueden procesar de manera eficiente esas secuencias de transformación. Es posible expresar cada una de las transformaciones básicas en la forma de matriz general con las posiciones de coordenadas P y P’ representadas como columnas de vector.2.15.P'=M1·P+M

 

 

 

 

2.1. Transformaciones bidimensionales

Traslación

Se aplica una traslación en un objeto para cambiar su posición a lo largo de la trayectoria de una línea recta de una dirección de coordenadas a otra. Convertimos un punto bidimensional al agregar las distancias de traslación, tx y ty la posición de coordenadas original (x,y)

El par de distancia de traslación se llama vector de traslación o vector de cambio. Se pueden expresar las ecuaciones anteriores en una sola ecuación matricial al utilizar vectores de columna para representar las posiciones de coordenadas y el vector de traslación

Los polígonos se trasladan al sumar el vector de traslación a la posición decoordenadas de cada vértice y se vuelve a generar el polígono utilizando un nuevo conjuntode coordenadas y vértices y las especificaciones actuales de los atributos.

 

 

 

 

 

 

 

 

 

Rotación

Se aplica una rotación bidimensional en un objeto al cambiar su posición a lo largo de la trayectoria de una circunferencia en el plano de xy . Para generar una rotación, especificamos un ángulo de rotación θ y la posición (x r , y r ) del punto de rotación (o punto pivote) en torno al cual se gira el objeto.

 

 

 

 

 

 

 

 

 

 

 

Escalación

Una transformación de escalación altera el tamaño de un objeto. Se puede realizar esta operación para polígonos al multiplicar los valores de coordenadas (x, y) de cada vértice por los factores de escalación s x y s  y para producir las coordenadas transformadas (x’, y’ )

2.2. Coordenadas homogéneas y representación matricial

En las aplicaciones de diseño y de creación de imágenes, realizamos traslaciones, rotaciones y escalaciones para ajustar los componentes de la imagen en sus posiciones apropiadas. En este tema consideramos cómo se pueden volver a formular las representaciones de la matriz de modo que se pueden procesar de manera eficiente esas secuencias de transformación. Es posible expresar cada una de las transformaciones básicas en la forma de matriz general con las posiciones de coordenadas P y P’ representadas como columnas de vector.2.15.P'=M1·P+M

2.3. Composición de transformaciones bidimensionales

Con las representaciones de matriz del tema anterior, podemos establecer una matriz para cualquier secuencia de transformaciones como una matriz de transformación compuesta al calcular el producto de la matriz de las transformaciones individuales. La creación de productos de matrices de transformación a menudo se conoce como concatenación o composición de matrices.

Traslaciones, rotaciones y escalaciones Traslaciones Se se aplican dos vectores de traslación sucesivos (tx1, t y1) y (tx2 , t  y2 ) en la posición de coordenadas P, la localización transformada final P, la localización transformada final P’ se calcula como:2.23.P'=T(t x2,t2)·T(tx1,ty1)·P}{=T(tx2, 2)·T(t x1,t y1)}{·P

Donde se representan P y P’ como vectores de columna de coordenadas homogéneas. Podemos verificar este resultado al calcular el producto de la matriz para las dos agrupaciones asociativas. Asimismo, la matriz de transformación compuesta para esta secuencia de transformaciones.

Rotaciones

Dos rotaciones sucesivas que se aplican en el punto P producen la posición transformada 2.26.P'=R(θ2)·R(θ1){·P}=R(θ2){· (θ1)}·P

Al multiplicar las dos matrices de rotación, podemos verificar que dos rotaciones sucesivas son aditivas

Rotación del punto pivote general

Con un paquete gráfico que sólo ofrezca una función de rotación para girar objetos con respecto del origen de las coordenadas, podemos generar casi cualquier punto pivote seleccionado (xr, yr)  al realizar la siguiente secuencia de operaciones de traslación-rotación-traslación:

1. Traslade el objeto de modo que se mueva la posición del punto pivote al origen de las coordenadas.

2. Gire el objeto con respecto del origen de las coordenadas

 

 

 

 

Escalación del punto fijo general

La siguiente figura ilustra una secuencia de transformación para producir escalación con respecto de una posición fija seleccionada (xf,f) al utilizar una función de escalación que sólo puede escalar en relación con el origen de las coordenadas

 

 

 

 

 

 

 

 

 

 

 

Propiedades de concatenación

La multiplicación de matrices es asociativa. Para tres matrices cualesquiera A, B y C, el producto matricial A·B·C se puede llevar a cabo al multiplicar primero a por B o multiplicar primero B por C:2.35.A · BC=( A· B)·C =A·( B·C)

Por tanto, podemos evaluar los productos matriciales al utilizar una agrupación asociativa ya sea de izquierda a derecha o de derecha a izquierda. Por otro lado, los productos de la transformación tal vez no sean conmutativos. En general el producto matricial A·B no es igual que B·A. Esto significa queremos trasladar y girar un objeto, debemos tener cuidado sobre el sentido en que se evalúa la matriz compuesta.

2.4. Transformación ventana-área de vista

Algunos paquetes gráficos permiten que el programador especifique coordenadas de primitivas de salida en un sistema de coordenadas de mundo de punto flotante, usando las unidades que sean relevantes para el programa de aplicación: angstroms, micras, metros, millas, años luz, etcétera. Se emplea el término de mundo porque el programa de aplicación representa un mundo que se crea o presenta interactivamente para el usuario.

2.6. Representación matricial de transformaciones tridimensionales

Así como las transformaciones bidimensionales se pueden representar con matrices de3 X 3 usando coordenadas homogéneas, las transformaciones tridimensionales se pueden representar con matrices de 4 X 4, siempre y cuando usemos representaciones de coordenadas homogéneas de los puntos en el espacio tridimensional. Así, en lugar de representar un punto como (x, y, z), lo hacemos como (x, y, z, W), donde dos de estos cuádruplos representan el mismo punto si uno es un multiplicador distinto de cero del  otro: no se permite el cuádruplo (0, 0, 0, 0). Como sucede en el espacio bidimensional, la representación estándar de un punto.

2.7. Composición de transformaciones tridimensionales

En este apartado se analizará la forma de componer matrices de transformación tridimensionales usando un ejemplo. El objetivo es transformar los segmentos de línea dirigida

 P1P2yP1P3 en la figura 2.18 de su posición inicial en la parte (a) a su posición final en la parte (b). De esta manera, el punto P1 se trasladará al origen P1P2 quedará en el eje positivo y P1P3

 Quedará en la mitad del eje positivo del plano (x, ). Las longitudes de las líneas no se verán afectadas por la transformación.

Las transformaciones entre sistemas de coordenadas cartesianos se llevan a cabo con una secuencia de transformaciones traslación. Rotación que hacen que los dos sistemas coincidan. Especificamos el origen de coordenadas y vectores de eje para un marco de referencia respecto al marco de referencia original. En un sistema bidimensional, un vector define completamente las direcciones del eje de coordenadas; pero en un sistema tridimensional, hay que especificar dos de las tres direcciones de los ejes. Las transformaciones geométricas son transformaciones afines. Esto es, pueden expresarse como una función lineal de posiciones de coordenadas. Traslación, rotación y escalación son transformaciones afines. Transforman líneas paralelas en líneas paralelas y posiciones de coordenadas finitas en posiciones finitas.

________________________________________________________

Conceptos para  glosario de términos de la unidad

Coordenadas Homogéneas

En matemáticas, y más concretamente en geometría proyectiva, las coordenadas homogéneas son un instrumento usado para describir un punto en el espacio proyectivo. Fueron introducidas por el matemático alemán August Ferdinand Möbius en el año 1837.

También pueden usarse como un sistema alternativo de coordenadas para trabajar en el espacio euclídeo, pues éste puede verse como un subconjunto del espacio proyectivo. De ese modo, las coordenadas homogéneas son ampliamente usadas en infografía para la representación de escenas en tres dimensiones. Su notación en forma matricial se emplea en bibliotecas de programación gráfica en 3D como OpenGL y Direct3D.

En coordenadas homogéneas, todo punto bidimensional está definido por tres coordenadas. De tal modo que un punto de dimensiones x, y, se lo representa por la terna: x / w, y / w, w.

Matemáticamente, las coordenadas x y y se hallan dividiendo los dos primeros números entre el tercero, respectivamente.

En dos dimensiones, su valor se puede encontrar más fácilmente si w = 1, por simplificación. En tres dimensiones, suele ocurrir lo mismo w = 1.

Básicamente, se trata de ampliar el plano euclídeo (en el caso bidimensional) al plano proyectivo, es decir, incluirle los puntos impropios o del infinito.

Así, un punto impropio es aquel donde w = 0.

Una consecuencia de esta escritura es que un punto propio tiene infinitas formas de escribirlo, todo dependerá de los cocientes x / w y y / w (con w distinto de 0). pila o stack( en programación)

Una pila (stack en inglés) es una lista ordinal o estructura de datos en la que el modo de acceso a sus elementos es de tipo LIFO (del inglés Last In First Out, último en entrar, primero en salir) que permite almacenar y recuperar datos. Esta estructura se aplica en multitud de ocasiones en el área de informática debido a su simplicidad y ordenación implícita de la propia estructura.

Para el manejo de los datos se cuenta con dos operaciones básicas: apilar (push), que coloca un objeto en la pila, y su operación inversa, retirar (o desapilar, pop), que retira el último elemento apilado.

En cada momento sólo se tiene acceso a la parte superior de la pila, es decir, al último objeto apilado (denominado TOS, Top of Stacken inglés). La operación retirar permite la obtención de este elemento, que es retirado de la pila permitiendo el acceso al siguiente (apilado con anterioridad), que pasa a ser el nuevo TOS. Por analogía con objetos cotidianos, una operación apilar equivaldría a colocar un plato sobre una pila de platos, y una operación retirara retirarlo. 

Las pilas suelen emplearse en los siguientes contextos:

      Evaluación de expresiones en notación postfija (notación polaca inversa).

      Reconocedores sintácticos de lenguajes independientes del contexto

     Implementación de recursividad.

2.1 Generación de líneas rectas

Linea

Una marca delgada hecha por un esferográfico o un lápiz etc.

En geometría una línea:

· es recta (sin curvas),
· no tiene grosor, y
· se extiende en ambas direcciones sin tener un final (infinitamente).

Si tuviera fin se llamaría "segmento de línea".

"Línea" normalmente significa recta, así que di "curva" si tiene una curva.

Algoritmo DDA para Generacion de Rectas

Algoritmo DDA para generación de líneas
Como todos saben Open GL es una herramienta que nos facilita mucho la generación de gráficos por computadora. Aqui aplicamos conocimientos matemáticos, usando Open GL para generar rectas, corcunferencias, elipses, etc.

DDA: El Algoritmo DDA es un algoritmo de línea de conversión de rastreo que se basa en el cálculo ya sea en el incremento de X o en el incremento de Y. La finalidad de este algoritmo es determinar los valores enteros correspondientes más próximos a la trayectoria de la línea para la otra coordenada.

  

 

Código:

void DDA(int x0,int y0,int xFin,int yFin)

{

int dx = xFin - x0, dy = yFin - y0, steps, k;

float xIncremento, yIncremento;

float x = x0, y = y0;

if (fabs (dx) > fabs (dy))

steps = fabs (dx); /* |m|<1>

else

steps = fabs (dy); /* |m|>=1 */

xIncremento=float(dx)/float (steps);

yIncrement = float (dy) / float (steps);

setPixel (round (x), round (y));

for (k = 0; k <>

{

x += xIncremento;

y += yIncremento;

setPixel (round (x), round (y));

}

}

BRESENHAM:

 

El algoritmo de Bresenham sirve para trazar una línea entre dos puntos.

 

 

 

Código:

void Bres(int x0,int y0,int xFin,int yFin)

{

int dx = fabs(xFin - x0),

dy = fabs(yFin - y0);

int p = 2 * dy - dx;

int dosDy = 2 * dy,

dosDyMenosDx = 2 * (dy - dx);

int x, y;

/* Determinamos que punto usamos como inicio. */

if (x0 > xFin) {

x = xFin;

y = yFin;

xFin = x0;

}

else {

x = x0;

y = y0;

}

setPixel (x, y);

while (x <>

x++;

if (p <>

p += dosDy;

else {

y++;

p += dosDyMenosDx;

}

setPixel (x, y);

}

}

 

 

Circunferencia

La circunferencia es una línea curva, plana y cerrada

La circunferencia sólo posee longitud. Se distingue del círculo en que éste es el lugar geométrico de los puntos contenidos en una circunferencia determinada; es decir, la circunferencia es el perímetro del círculo cuya superficie contiene.

Puede ser considerada como una elipse de excentricidad nula, o una elipse cuyos semiejes son iguales. También se puede describir como la sección, perpendicular al eje, de una superficie cónica o cilíndrica, o como un polígono de infinitos lados, cuya apotema coincide con su radio.

La circunferencia de centro en el origen de coordenadas y radio 1 se denomina circunferencia unidad o circunferencia goniométrica

Algoritmo de Bresenham para trazar circunferencias

El programa debe trazar un circulo cada que el usuario agregue dos puntos.

El usuario debe introducir con el ratón dos puntos p0 y p1 para trazar el circulo. El primero, que representa el centro

del circulo p0 = (cx; cy) y el segundo, desde el cual se puede calcular el radio d(p0; p1) = r. Es decir, el primero es el

centro y el otro es un punto en la circunferencia.

 

 

Se deben de poder trazar círculos parciales. Es decir, puede suceder que algunos de los puntos del circulo caigan

fuera de la pantalla, en ese caso el programa debe de poder trazar la parte visible del circulo.

Sugerencia para mejorar el programa. Por calificación extra puede tratar de generalizar el algoritmo de Bresenham

para que pueda trazar elipses (El algoritmo solo funciona para trazar elipses alineadas a los ejes). Recuerde que si en clase

se dedujo el algoritmo del circulo a partir de la ecuación x2 + y2 = r2, se puede deducir el de la elipse a partir de la

ecuación􀀀 x a_2􀀀 yb_2= 1. Donde a y b son los radios de la elipse con respecto a los ejes.

Puede consultar como bibliografía [2] Y para darse idea de como se puede hacer la interfaz de usuario puede ver como

operan los programas como Inkscape o Ilustrator el trazo de círculos y elipses. Con esto en mente puede intentar el trazador

de elipses a mano alzada. Usando las funciones glutMotionFunc y glutActiveMotionFunc.